
「考えることから始める」には、簡単なことから始めるのが鉄則です。
例えば
4×5=20
×(掛け算)の記号を使わない方法は?
4+4+4+4+4=20
5+5+5+5=20
の2通りあるのは直ぐに理解できますよね?
でも急に
a×a+b×b=c×c
はピタゴラスの定理ですが、
内接円を用いた証明は・・・・
と書かれると、それぞれの名前の意味を調べて覚えることから始めないと、「考える」ところまでたどり着かないと思います。
コンピュータも同じ。「考えることから始める」には、コンピュータの最も簡単な部分から始めるのがベストです。
ではさっそく始めてみましょう。
内容を細かく覚えずに、どんどん進んで行きましょう。
ここでは「白板」を使います。これに色々書き込むことから始めます。
これは縦11横11の計121個にレ点が付けられる白板です。コンピュータになる前の原型と考えて下さい。
これを使って色々考えて行きます。これはHTMLを使ったもので、ホームページを開ける環境のPCならば、簡単に使えるツールです。

これは白板なので、情報を書き込むことができます。私は例として「5」という数字を書き込んでみました。皆さんも好きな数字を書き込んでみてください。
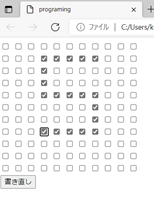
通常ペンで字を書くと連続した線で5が描かれます。でもこれは「レ点の有/無」だけで5を表現しています。
連続した線で描かれたものを「アナログ」、上記のように「レ点有/無=on/off」で表現する方法を「デジタル」と言います。
コンピュータはこのように「デジタルで情報を記憶」することが全てのベースになります。
ここでは1つの数字を情報として白板に描きました。では、数字をこの白板上に何個記憶させることができるでしょう?考えて、できるだけ多く記入してみて下さい。

上の例では一つの数字に3行5列を使い、「1」「2」「3」「4」「5」「6」の数字を表しています。6つの一桁の数「1,2,3,4,5,6」を記憶させる装置ができました。
また、6桁の数字「123456」を記憶させる装置にもできます。
でもその場合、数字は上側3個、下側3個に分かれており、6桁の数字には見えないかもしれません。
そこでキチンと認識してもらえるように、利用する人に白板の読み方を教えておきましょう。
では、利用法を教える文章を考えてみて下さい。
解答例は
「この装置は6桁の数字を1つ記憶する装置です。上半分の左側から右側に6桁、5桁、4桁、下半分の左側から右側に3桁、2桁、1桁の数字を表しています。以下のように並べ替えると6桁の数字が表せます。」

このように、最初に「システム」を考える人は、その「システム」を使えるように、「利用法」を作ります。
この「システム」を利用する人は、その「利用法」を覚える必要があります。
プログラム言語も同じです。その「プログラム言語」を作った人が決めた「約束事」を「利用法」から学ぶことで、そのプログラム言語が使えるようになります。
この内容が複雑になればなるほど、「利用法」も複雑になるので、覚えることも多くなります。
プログラミングの学習で覚えることが多いのは、この「利用法」を知らないと、そのプログラミング言語を使えないという理由から。
複雑なプログラミングほど覚えることが多くなり、それだけで挫折しがちです。
でも、この「利用法」を使わないのならば、覚える必要はありません。
その代わり、上記例では「白板に数字を記憶させる」方法を自分で考える必要があります。
ではプログラミング言語の場合、最低何処まで覚えれば、プログラミングを楽しむことができるのでしょう?
順を追って、この白板をコンピュータに変えていきながら確認しましょう。
上の例では数字の形状を記憶させる方法でした。
でも、数字は横に並べて書きます。今回はそのことを考え、1行で数字を表す方法を考えましょう。
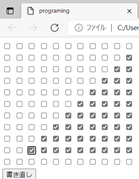
上記の例は10個の1桁の数字「0,1,2,3,4,5,6,7,8,9」を記憶した装置、もしくは10桁の数字「9876543210」を記憶した装置です。ではどういう「約束事」だと思いますか?考えてみて下さい。
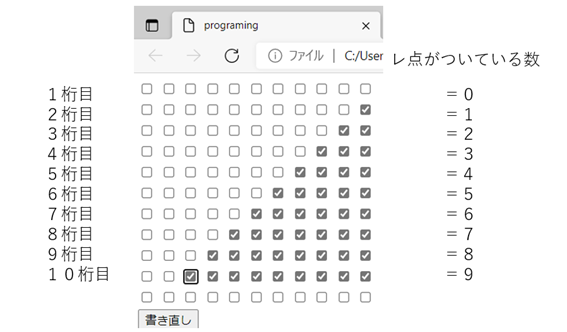
この「約束事」は「1行目=1桁~10行目=10桁」とします。各行の「レ点」が付いている数がその桁の数字を指します。
10桁から1桁まで左から横に並べると、「9876543210」の数字となります。
どうでしょう?最初の「数字の形状を記憶させる方法」よりも大きな数を記憶できるようになってきました。

これは別の「約束事」を使い、同じ10個の1桁の数字「0,1,2,3,4,5,6,7,8,9」を記憶した装置、もしくは10桁の数字「9876543210」を記憶した装置です。ではどういう「約束事」だと思いますか?考えてみて下さい。

10桁から1桁まで左から横に並べると、「9876543210」の数字となります。
皆さんもご存じの「マークーシート方式」ですね。列にも番号を付け、その番号に「レ点が付いていると、その数字を指す」という「約束事」です。
このように、白板に数字を記憶させる方法は数多く考えることができます。
その中で先人が選んだ方法が「2進法」です。理由は最も効率よく数字を記憶させることができるからです。
では2進法で上記と同じ数字を表してみましょう。
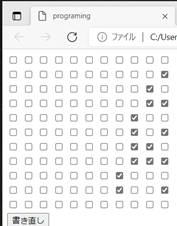
これで10個の1桁の数字「0,1,2,3,4,5,6,7,8,9」を記憶した装置、もしくは10桁の数字「9876543210」を記憶した装置です。
殆ど左側の□を使っていませんよね?
2進法について少し解説しましょう。
我々が普段使っているのは10進法。1桁目で、0,1,2,3,4,5,6,7,8,9まで数えると、1桁で表せる数字は9が最高なので、次は2桁目に1を入れ、1桁目を0に戻します。これが繰り上がりです。
これで、0,1,2,3,4,5,6,7,8,9,10となる訳ですね。
同じように考えます。□のレ点無=0,レ点有=1とした場合、1桁目は0,1まで数えると1桁で表せる数は1が最高なので、次は2桁目に1を入れ、1桁目を0に戻します。これが繰り上がりです。
これで、0,1,10となる訳ですね。10進数の10までを2進数で数えると、0,1,10,11,100,101,110,111,1000,1001,1010となります。
では改めて2進法を使った「約束事」を説明すると、
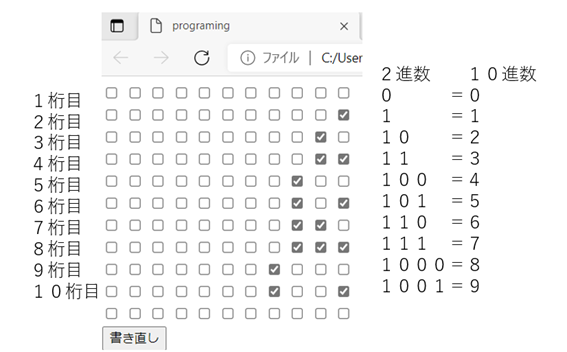
この「約束事」は「1行目=1桁~10行目=10桁」とします。各行の「レ点有=1」、「レ点無=0」として10進法の数字を2進法で表したものです。
10桁から1桁まで左から横に並べると、「9876543210」の数字となります。
でも、左側の□を全く使っていないので、勿体ないですよね。
もし上記の左側の□をフルに使ったら、1行だけで10進数でどの位の数まで表せるのでしょう?
その計算は□が11個ありますので、
2^10+2^9+2^8+2^7+2^6+2^5+2^4+2^3+2^2+2^1+2^0=2047
^は乗数を表す記号です。
ここまで大きな数が記憶できるならば、
この法則は「1行目=1番地~11行目=11番地の11カ所に0~2047までの数字を記憶できる装置」
に改めた方が良いですね。随分記憶内容が増えました。

上記の例では各番地に2進数で11111111111(10進数ならば2047)までの入力が可能です。
昔の人は、白板内で2進法で番地を決め、そこに2進法で数値を記憶する機能を白板に入れ込みました。
これで白板がコンピュータに変わります。
ではこの番地と値を詳しく見ていきましょう。
プログラミングでは上記の「番地=adress」と「値=data」を一まとめにして名前を付けます。
具体的には、何bitを使用するデータかをプログラム上で書き(宣言)し、名前を付けて使用します。
ではこのbitとは何でしょう?
「2者択一」の場合、例えば(on/off)、(男性/女性)、(既婚/未婚)、(真/偽)の情報は□一つでどちらか(レ点を付けるか付けないか)を選択できます。
この1つの□を1bit(ビット)と言います。
画像の色を表示する場合は、A(透明度)、R(赤)、G(緑)、B(青)の強度をそれぞれ□□□□□□□□=8bit(ビット)=1byte(バイト)で表します。
1byteは10進法では2^7+2^6+2^5+2^4+2^3+2^2+2^1+2^0=255
即ち、それぞれ0~255の値が入ります。
色を表す強度は「255段階あれば十分」と考えられていました。現在でも「色」を表示するのには、この1byteが利用されています。
プログラム上では書き方(宣言)は、
byte DATA1 = 10;
この文は「DATA1と名付けた場所にbyteの大きさ[8bit]の記憶場所を作ります。その記憶場所に10進法で10の値を入力します」という意味になります。
実際にコンピュータ上では、適当な番地に1byteのスペースを確保し、値として0001010が入力されます。
マシン語やc++などのプログラム言語では「番地」と「値」の両方を使用者が管理する必要があります。
でも、殆どのプログラム言語では、上記のようにDTAT1という名前を「宣言」するだけで、「番地」と「スペース」を気にする必要はありません。
プログラム言語の方で勝手に管理してくれます。
このようにしてプログラミングとは、プログラミング言語毎に決まった「書き方」を覚えて行きます。
中でも「記憶場所を作る」という作業はプログラムを行う上で、一番重要なことです。
ではbitの方はどう書くのでしょう
bit DATA2 = とは書きません。
boolean(又はbool) DATA2 = true;
と書きます。入力できるのはtrueとfalseの2種類です。「論理値」と言います。
「true」は「真」(正しい)、「false」は「偽」(違う)を意味します。
コンピュータ上は「on」、「off」が設定されます。
このようにコンピュータは2進法で色々処理されるのですが、我々は普段10進法に慣れていますので、面倒ですよね。
実はコンピュータはハードウェアで2進法での値を10進法での値に勝手に変換してくれる機能が付いています。
普段我々が使用する数字は整数と実数。それと文字。
以下の3つように定義します。
整数: int DATA3 = 10;
実数: float DATA4 = 10.0;
文字: string DATA5 = “こんにちは”;
入れた値(文字)はその後自由に書き換えることができます。よってこれを「変数」と呼びます。
c、c++、c#、Java等はすべて同じ書き方です。
変数については、以下の5つはしっかり覚えておきましょう。
boolean 好きな変数名 = 初期の論理値
byte 好きな変数名 = 初期の0~255値(javaは-128~127)
int 好きな変数名 = 初期の整数値
float 好きな変数名 = 初期の実数値
string 好きな変数名 = 初期の文字を“”で囲んで記載
(但し、何bitで構成されているかは若干相違があります。)
VBA(ビジュアルベーシック)は Dim intのようにDimを最初に書いて変数の「宣言」を行います。
Dim int 好きな変数名 = 初期の整数値
では次に変数名への変数の入れ方を確認しましょう。
この変数名への値の入れ方も上記言語では共通です。左が現在、右が過去の値です。「右の結果を左に入れる」という考え方です。
例:
変数名1 = 値1 [変数名1に値1を入れる]
変数名1 = 値1 + 変数名2[値1と変数名2に入った値を足して、その足した値を変数名1に入れる]
変数名1 = 値1 + 変数名1[値1と変数名1に入った値を足して、その足した値を変数名1に入れる]
この変数名に入っている値の書き換え方も重要です。同様に左が現在、右が過去の値です。これも覚えましょう。
次に四則計算(+-×÷)の書き方も重要です(右は値1でもOK)。
変数名1 = 変数名1 + 変数名2 [足し算]
変数名1 = 変数名1 - 変数名2 [引き算]
変数名1 = 変数名1 * 変数名2 [かけ算]
変数名1 = 変数名1 / 変数名2 [割り算]
では、今まで覚えたことで簡単なプログラミングを行いましょう。
「変数r1に整数3、変数r2に整数5を入れて、その足し算の結果を変数r3に書き込みなさい」
やってみましょう。
整数だから使うのはint
//ここは宣言部分です
int r1 = 3
int r2 = 5
int r3
//ここは計算部分です
r3 = r1 + r2
できましたか?
c#の場合、//はコメント欄です。プログラムとしては無視されます。
アルファベットと数字、記号の羅列だと判り難いので、プログラミングではこのようにコメントを入れるのが重要となります。
では次の問題。
「変数r1に整数3、変数r2に整数5を入れて、そのかけ算の結果を変数r3に書き込みなさい」
やってみましょう。
整数だから使うのはint
式1)
//ここは宣言部分です
int r1 = 3
int r2 = 5
int r3
//ここは計算部分です
r3 = r1 * r2
できましたか?では応用問題です。
「変数r1に整数3、変数r2に整数5を入れて、そのかけ算の結果を変数3に書き込みなさい。但し、プログラム内で*の記号を使ってはいけません」
やってみましょう。
式2)
//ここは宣言部分です
int r1 = 3
int r2 = 5
int r3
//ここは計算部分です。*が使えないので、r1を5回加算しています
r3 = r1 + r1 + r1 + r1 + r1
確かに3*5=3+3+3+3+3です。
答えは合っていますが、r2=5が入っていませんよね?
ここで次に覚えることが繰り返し計算です。
「3*5」を言葉で説明すると、
「3を繰り返し5回足せば良い」と言い表せます。この「繰り返し」を「for文」を使って表します。
式3)
//ここは宣言部分です
int r1 = 3;
int r2 = 5;
int r3 = 0;
//ここは計算部分です。for文で、{ }内を5回繰り返しています。iはカウンターでループ毎に値が1ずつ増えていきます
for(int i = 1; i <= r2; i = i + 1)
{
r3 = r3 + r1;
}
()内の意味は「変数名iに整数1を代入する。iがr2の値以下ならば{}の中の処理を繰り返す。{}を1回繰り返す度にiの値を1ずつ増やしていく」となります。
i <= r2 を論理式と言います。種類は
変数1 <= 変数2 変数1の値が変数2以下の場合「真」
変数1 < 変数2 変数1の値が変数2より小さい場合「真」
変数1 >= 変数2 変数1が変数2以上の場合「真」
変数1 > 変数2 変数1が変数2より大きい場合「真」
変数1 == 変数2 変数1が変数2と等しい場合「真」
変数1 != 変数2 変数1が変数2と等しくない場合「真」
です。
上記の「for文」の書き方はc#という言語です。他の言語は若干書き方が違いますが、「for文」が繰り返し文であることは多くの言語が共通です。
次に「3*5」を別の言葉で言ってみましょう。
「3を繰り返し足していくが、もしも5回足したら計算を止める」とも言い表せます。
この「もしも」は「if文」を使って表します。
式4)
//ここは宣言部分です
int r1 = 3;
int r2 = 5;
int r3 = 0;
//for文で、{ }内を1000回繰り返します。iはカウンターでループ毎に値が1ずつ増えていきます
for(int i = 1; i <= 1000; i = i + 1)
{
//計算部分です
r3 = r3 + r1;
//if文です。iの値がr2と等しくなったら{ }内のberakでforループから抜けます
if (i == r2)
{
break;
}
}
上記のプログラムでは「for文」だけだと、変数iが1000以下の間は{}内の処理を実行し続けます。
その中に「if文」で()内は、iがr2と等しくなったら{}内の処理を実行しなさい。
という意味になります。{}内のbreak;は「for文」の繰り返しを止めて外にでるという命令になります。
{}はc#の場合、分かり易いように位置をずらして表示してくれます。
如何でしょうか?
式1)、式2)、式3)、式4)は全て「3×5=15」を求める式ですが、4通りのプログラミングが考えられるのです。
あなたの「考え方」次第で、いくらでもそれ以外のオリジナルのプログラミングができるのです。
プログラミングの基礎中の基礎は以上です。
これだけ覚えておけば、直ぐにあなたも「考えるプログラミング」を始めることができます。